算法一-6月24

一、正则表达式匹配

（1）略解

原链接：https://mp.weixin.qq.com/s/Khts_1iw--oWPxe0f4AoMg

题目：给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

• . 匹配任意单个字符
• * 匹配零个或多个前面的那一个元素

简单来说：就是实现 . 和 * 的功能。普通的两个字符串比较，涉及到 KMP 算法。

可以使用动态规划，其符合 最优子结构性质 ，因为 s 匹配 p，按照规则得到的 s 子串和 p 子串肯定也匹配。

• 状态定义：f(i,j) 代表 s 中以 i 下标为结尾的子串和 p 中的以 j 下标为结尾的子串是否匹配。
• 状态转移：也就是我们要考虑 f(i,j) 如何求得，前面说到了 p 有三种字符，所以这里的状态转移也要分三种情况讨论：

1. 如果字符规律的下一个字符， p[j] 为普通字符，则在 s 子串匹配 p 子串的基础上，再判断 p 子串的下一个字符和 s 子串的下一个字符是否相等。即 f(i,j) = f(i - 1, j - 1) && s[i] == p[j] 。在表格上就是取左上对角的值。
2. 如果 p[j] 为 . ，则代表 s 串的某个字符无论是什么，都可以匹配。即 f(i,j) = f(i - 1, j - 1) && p[j] == '.' 。在表格上就是取左上对角的值。
3. p[j] 为 *：必须先读得上一个字符，即 p[j - 1] 的字符，例如为字符 a。然后根据 a* 实际匹配 s 中 a 的个数是 0 个 或者多个。
   • 当是 0 个的时候，则这两个字符串没有用，f[i][j] 等于 f[i][j-2] 。
   • 当是多个的时候，则只需要判断 s[i] 和 p[j-1] 是否相等，以及在加入 s[i] 字符之前的情况，即 f[i-1][j]。

---

第 1 点和第 2 点写出代码，两个条件合并了，因为结构类似：

• s[i] == p[j] 相当于普通字符比较相等
• p[j] == '.' 相当于 p[j] 是 . 字符

if (i - 1 >= 0 && p[j] != '*') {
  f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
}

第 3 点写出代码：

• 或条件的左边，代码第 2 行：当 * 匹配 0 个字符，直接取 f[i][j - 2] 的值
• 或条件的右边：当 * 匹配 多个字符，需要满足两个条件
  • f[i - 1][j] ：代表 s 子串加上 s[i] 之前是否匹配，只有之前匹配了才有机会加多一个字符来看是否匹配 p 串。
  • (s[i] == p[j - 1] || p[j - 1] == '.') ：判断 p[j-1] 与 s[i] 是否匹配，若匹配了，则 f[i][j] 才匹配。

else if (p[j] == '*') { 
  f[i][j] = (j - 2 >= 0 && f[i][j - 2]) || 
    (i - 1 >= 0 && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.'));
}

（2）详解

动态规划的核心就是填表格。下面假设 s 串为 aab ，p 串为 c*a*b 。下面是空表。

	p	_	c	*	a	*	b
s		0	1	2	3	4	5
_	0	√
a	1
a	2
b	3

为了好写循环代码，所以在两个字符串之前都加上一个空格。 s[0] 和 p[0] 都相当于空串。

然后 s 串的第一个字符不动， p 串从第二个字符开始循环，即字符串不变，字符规律在变。

1. 第 2 个字符是 c ，但其后面是 * 号，则进入下一个循环
2. 第 3 个字符是 * ，由于 s 串是第 1 个字符，是空串，不等于 c，所以继续看去掉 c* 两个字符后是否匹配，很明显 f[0][2] = f[0][0] = true。所以表格填充成如下：

	p	_	c	*	a	*	b
s		0	1	2	3	4	5
_	0	√	x	√
a	1
a	2
b	3

3. 以此类推，得出后面 a* 的匹配状态，然后 b 不等于 空串，所以不匹配，则第一行的填表结果如下。

	p	_	c	*	a	*	b
s		0	1	2	3	4	5
_	0	√	x	√	x	√	x
a	1
a	2
b	3

4. 然后开始填写第 2 行，s [1] 为 a 字符。
   1. a 不等于 p[0] 空串，不匹配，所以 f[1][0] = false；
   2. p[1] 的下一个是 * 号，则跳过；
   3. p[2] 是 * 号，然后比较 p[1] 和 s[1] ，p 的第 1 个字符——c 不等于 s 的第 1 个字符——a，所以不匹配。得出下面表格结果。

	p	_	c	*	a	*	b
s		0	1	2	3	4	5
_	0	√	x	√	x	√	x
a	1	x	x	x
a	2
b	3

5. 然后看 p 的第 3 个字符，因为 p 的第 3 个字符 是 * 号，所以 p[3] 跳过；
   1. 看 p 的第 4 个字符，是 * 号，然后看 p 的第 3 个字符 是否等于 s 的第 1 个字符 ，两个都是 a 字符，所以相等；
   2. 接着看 f[i-1][j] 是否匹配，即看该格的上面是否是对勾，f[0][4] 是对勾所以 f[1][4] 也是对勾。结果如下表所示。

	p	_	c	*	a	*	b
s	f(i,j)	0	1	2	3	4	5
_	0	√	x	√	x	√	x
a	1	x	x	x	x	√	x
a	2
b	3

6. 然后一点点将表格填写完整，最后得出两个字符串匹配。

	p	_	c	*	a	*	b
s		0	1	2	3	4	5
_	0	√	x	√	x	√	x
a	1	x	x	x	x	√	x
a	2	x	x	x	x	√	x
b	3	x	x	x	x	x	√

（3）总结

动态规划算法不难理解，但需要找到状态如何转移。

全部代码：

public static boolean isMatch(String ss, String pp) {
  // 技巧：往原字符头部插入空格，这样得到 char 数组是从 1 开始，而且可以使得 f[0][0] = true，可以将 true 这个结果滚动下去
  int n = ss.length(), m = pp.length();
  ss = " " + ss;
  pp = " " + pp;

  // 将字符串转化为字符数组
  char[] s = ss.toCharArray();
  char[] p = pp.toCharArray();

  // f(i,j) 代表 s 中的 1~i 字符和 p 中的 1~j 字符 是否匹配
  boolean[][] f = new boolean[n + 1][m + 1];

  // 初始化第1个数
  f[0][0] = true;

  for (int i = 0; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      // 如果下一个字符是 '*'，则代表当前字符不能被单独使用，跳过
      if (j + 1 <= m && p[j + 1] == '*')
        continue;

      // 对应了 p[j] 为普通字符和 '.' 的两种情况
      if (i - 1 >= 0 && p[j] != '*') {
        f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
      }

      // 对应了 p[j] 为 '*' 的情况，一种情况是不看这两个字符，另一种是看p[j-1]与s[i]是否相等
      else if (p[j] == '*') {
        f[i][j] = (j - 2 >= 0 && f[i][j - 2])
          || (i - 1 >= 0 && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.'));
      }
    }
  }
  return f[n][m];
}

二、回文数

原文链接：https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=2&sn=4bc0ec832d90ca5cf6dbdea95560d6a9&chksm=fd9ca9fdcaeb20ebe1c29592afb103ee4120ea5aa32c1036d5f3142757c8a2431705ef2e6b57&scene=178&cur_album_id=1715134171561410565#rd

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1:

• 输入: 121

• 输出: true

示例 2:

• 输入: -121
• 输出: false
• 解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3:

• 输入: 10
• 输出: false
• 解释: 从右向左读, 为 01 。因此它不是一个回文数。

（1）略解

最简单的一种解法就是将数字转换为字符串，然后跟原来的进行比较。

class Solution {
  public boolean isPalindrome(int x) {
    String s = String.valueOf(x);
    StringBuilder sb = new StringBuilder(s);
    sb.reverse();
    return sb.toString().equals(s);
  }
}

另一种非字符串解法，就是 让数字完全翻转。新的整数的数字是从旧的整数的个位开始的。

• 第 3 行：如果是负数，其必不是回文数
• 第 4 行：原来的是 int 数据类型，其范围为 -2³¹ (-2147483648) ~ 2³¹-1 (2147483647) ，如果反转了，有溢出风险，所以使用 long 数据类型。 2⁶⁴ (-9223372036854775808)~ 2⁶⁴-1(9223372036854775807)
• 第 6 ~ 9 行：然后不断的对 x 取余得出个位数，然后将反转的数左移（乘10）并加上个位数。

class Solution {
  public boolean isPalindrome(int x) {
    if (x < 0) return false;
    long ans = 0;
    int t = x;
    while (x > 0) {
      ans = ans * 10 + x % 10;
      x /= 10;
    }
    return ans - t == 0;
  }
}

如果不能使用 long 数据类型的话，则需要使用到回文数的特性，左右部分相等。收集右半部分和反转整数一个思路。

• 第 4 行：如果是负数或者末尾是 0 的话，肯定不是回文数。
• 第 6 行： x 是否大于 t 来作为左右分隔的条件，这样不用计左右部分数字的个数，不过可能会导致 t 的数字个数会比 x 的数字个数 多一位。
• 第 12 行：判断的时候不仅要比较 x 和 t，还要比较 x 和去掉一位的 t 。

class Solution {
  public boolean isPalindrome(int x) {
    // 对于 负数 和 x0、x00、x000 格式的数，直接返回 flase
    if (x < 0 || (x % 10 == 0 && x != 0)) return false;
    int t = 0;
    while (x > t) {
      t = t * 10 + x % 10;
      x /= 10;
    }
    // 回文长度的两种情况：直接比较 & 忽略中心点（t 的最后一位）进行比较
    return x == t || x == t / 10;
  }
}

三、工程模拟题

原题链接：https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=3&sn=9b23784134bdce0cc003b9b28d273e7f&chksm=fd9ca9fdcaeb20eb0faa62eb5543208f2152147b4c3369824f0a2e87d0fb56553ba8f66d11b1&cur_album_id=1715134171561410565&scene=189#wechat_redirect

请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符。

接下来的转化规则如下：

• 如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。
• 假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。
• 该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0 。

提示：

• 0 <= s.length <= 200
• s 由英文字母（大写和小写）、数字、' '、'+'、'-' 和 '.' 组成

示例 1：

• 输入: "42"
• 输出: 42

示例 2：

• 输入: "-42"
• 输出: -42
• 解释: 第一个非空白字符为 ' - '，它是一个负号。我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42。

示例 3：

• 输入：" 4193ssss "

• 输出: 4193

• 解释: 转换截止于数字 ' 3 ' ，因为它的下一个字符不为数字

示例 4：

• 输入：“ w3029 ”

• 输出: 0

• 解释: 第一个非空字符是 'w', 但它不是数字或正、负号。因此无法执行有效的转换

示例 5:

• 输入: "-91283472332"
• 输出: -2147483648
• 解释: 数字 "-91283472332" 超过 32 位有符号整数范围。 因此返回 INT_MIN (−231)

（1）略解

首先对题目进行分析：

1. 去掉字符串的前导空格
2. 第一个字符只能是 - 、+ 和 数字
3. 然后继续向后匹配字符，直到遇到非数字字符。其过程需要注意数字是否越界。

下面为代码：

• 第 11 ~ 16 行：去掉字符串的前导空格
• 第 18 ~ 28 行：判断第一个字符
• 第 30 ~ 41 行：判断当前数字是否超过最大值，不能直接将当前数字与 Integer.MAX_VALUE 比较，因为如果当前数字超过最大值会程序报错，不会进行比较。所以需要将思维逆转，将 Integer.MAX_VALUE 降一位再进行比较。 ans * 10 + cur > Integer.MAX_VALUE 相当于 ans > Integer.MAX_VALUE - cur / 10

class Solution {
  public int myAtoi(String s) {
    // n 代表整个字符的长度
    int n = s.length();
    
    char[] chars = s.toCharArray();
    
    // 当前取到的字符的下标
    int idx = 0;       

    // 去除前导空格，如果去完前导空格后无字符了，返回 0
    // 不断地将下标移动到后面，直到遇到不是空格为止
    while (idx < n && chars[idx] == ' '){
      idx++;
    }
    if (idx == n) return 0;

    // 检查第一个字符：可以为正负号/数字
    // isNeg代表该数是负数
    boolean isNeg = false;
    if (chars[idx] == '-') {
      idx++;
      isNeg = true;
    } else if (chars[idx] == '+') {
      idx++;
    } else if (!Character.isDigit(chars[idx])) {
      return 0;
    } 

    int ans = 0;
    while (idx < n && Character.isDigit(chars[idx])) {
      // 将当前的字符转换为数字
      int cur = chars[idx++] - '0';
      // 防止 ans = ans * 10 + cur 溢出
      // 等价变形为 ans > (Integer.MAX_VALUE - cur) / 10 进行预判断
      if (ans > (Integer.MAX_VALUE - cur) / 10) {
        // 如果是负数则返回最小值，否则返回最大值
        return isNeg ? Integer.MIN_VALUE : Integer.MAX_VALUE;
      }
      ans = ans * 10 + cur;
    }
    // 返回最终结果数字
    return isNeg ? -ans : ans;
  }
}

四、Z字形变换

原题链接：https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=4&sn=9dee24011b1ff7814aac348d94c00460&chksm=fd9ca9fdcaeb20eb81af16d22fdfb514e9e7bd75cd5af07da157a51275e97223c265240ae6b6&cur_album_id=1715134171561410565&scene=189#wechat_redirect

将一个给定字符串 s 根据给定的行数 numRows ，以 先从上往下、再从左到右 进行 Z 字形排列。

比如输入字符串为 PAYPALISHIRING 行数为 3 时，排列如下。然后 先从左到右、再从上往下，组成一个新的字符串，PAHNAPLSIIGYIR 。

P     A     H     N
A  P  L  S  I  I  G
Y     I     R  

请你实现这个将字符串进行指定行数变换的函数：String convert(string s, int numRows) ；

• 输入：s = PAYPALISHIRING, numRows = 4
• 输出：PINALSIGYAHRPI
• 解释：

P       I       N
A    L  S    I  G
Y  A    H  R
P       I 

（1）略解

第一种解法就是直接计算每一个字符的偏移量，很直接，但比较麻烦。

1. 每个字符到达下一个字符，会有两种方向，从上到下，或者从下到上。例如第 2 行，从 A 到 L，从下到上，经过 YPA 三个字符；从 L 到 S ，从上到下，经过 I 一个字符。
2. 需要计算不同行的两个方向所经过的字符数。除了第 1 行和最后 1 行，因为这两行的偏移量不会变。

每下面一行，两个相邻的字符的上面都会同时多出一个字符。即原来的从上到下偏移量 + 2，从下到上的偏移量，也是如此。所以 当前偏移量 = 当前行数 * 2 - 1

行数	从上到下的字符数	从下到上的字符数
2	1	3
3	3	1

P       I       N
A    L  S    I  G
Y  A    H  R
P       I 

3. 然后因为当前字符的下一个字符的方向都不一致，所以需要定义一个标记来进行反转方向。

---

下面为具体代码：

1. 第 11 ~ 18 行：对象第 1 行和最后 1 行，偏移量是固定的，都是 (总行数 - 1) * 2 - 1
2. 第 25 ~ 33 行：算出两个方向的偏移量
3. 第 35 ~ 41 行：轮流加上两个方向的偏移量就可以取到正确的字符

public static String convert(String s, int r) {
  // n代表字符串的长度
  int n = s.length();

  // 如果字符串只有1个字符或者只有排列1行，则直接返回原字符串
  if (n == 1 || r == 1)
    return s;

  StringBuilder sb = new StringBuilder();
  for (int i = 0; i < r; i++) {
    // 对于第1行和最后1行，偏移量是固定的
    if (i == 0 || i == r - 1) {
      int j = i;
      int rowOffset = (r - 1) * 2 - 1;
      while (j < n) {
        sb.append(s.charAt(j));
        j += rowOffset + 1;
      }
    } else {
      // 对于其他行，需要获取到当前字符到下一个字符的偏移量
      // 到下一个字符有2个方向，一个是从当前字符向上然后向下
      // 另一个是从当前字符向下然后向上
      int j = i;

      // 获取当前行是正数第几行
      int topRow = i;
      // 算出从当前字符向上到向下需要跨过多少字符
      int topOffset = topRow * 2 - 1;

      // 获取当前行是倒数第几行
      int bottomRow = r - i - 1;
      // 算出从当前字符向下到向上需要跨过多少字符
      int bottomOffset = bottomRow * 2 - 1;

      // 因为方向每次都需要反转，所以需要设置标记
      boolean flag = true;
      while (j < n) {
        sb.append(s.charAt(j));
        j += flag ? bottomOffset + 1 : topOffset + 1;
        flag = !flag;
      }
    }
  }
  return sb.toString();
}

（2）略解2

我们可以找规律直接算出下一个字符的下标。

• 对于第 1 行：P——0；I——6；N——12。首项为 0，公差为 6 —— 2 * ( r - 1 )

• 对于最后 1 行：P——3；I——9。首项为 r-1，公差为 6 —— 2 * ( r - 1 )

P       I       N
A    L  S    I  G
Y  A    H  R
P       I 

然后找中间行的规律：

• 对于第 2 行：A——1；L——5；S——7；I——11；G——13
• 对于第 3 行：Y——2；A——4；H——8；R——10

根据第 1 点的题解可以知道下一个字符有两个方向，在数学方面就是 等差数列交替排列。

可以看到第 2 行： 1(A) + 6 = 7(S) ；7(S) + 6 = 13(G)。5(L) + 6 = 11(I)。

第 3 行：2(Y) + 6 = 8(H) 。4(A) + 6 = 10(R)

两个等差数列的公差都是 6，即 2 * ( r - 1 )，然后就要计算出两个等差数列的首项。

• 第 1 个等差数列很明显首项是 i
• 第 2 个等差数列的首先需要计算一下：第 1 行的第 2 个字符（I）的下标是 2r - 2 ，而第 2 个等差数列的首项字符下标是在该基础上退后 i 个字符 ，例如第 2 行，回退 1 个字符（L）。所以得出第 2 个等差数列的首项是 2 * r - i - 2

得出下面代码：

public String convert(String s, int r) {
  // n为s字符串的长度
  int n = s.length();
  if (n == 1 || r == 1) return s;

  StringBuilder sb = new StringBuilder();
  
  // 对每一行进行遍历
  for (int i = 0; i < r; i++) {
    // 第1行和最后1行的情况
    if (i == 0 || i == r - 1) {
      int pos = i;
      // 计算出偏移量
      int offset = 2 * (r - 1);
      while (pos < n) {
        sb.append(s.charAt(pos));
        pos += offset;
      }
    } else {
      // 得出两个等差数列的首项
      int pos1 = i, pos2 = 2 * r - i - 2;
      // 得出两个等差数列的公差
      int offset = 2 * (r - 1);
      
      // 当两个下标都同时超出字符串长度，证明已经到当前行的末尾
      while (pos1 < n || pos2 < n) {
        if (pos1 < n) {
          sb.append(s.charAt(pos1));
          pos1 += offset;
        }
        if (pos2 < n) {
          sb.append(s.charAt(pos2));
          pos2 += offset;
        }
      }
    }
  }
  return sb.toString();
}

五、找出两个数组合并后的中位数

原题链接：https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=5&sn=de027e77fd0cc185bd5d753bab38f5d0&chksm=fd9ca9fdcaeb20eb2d70190b3240d69ebc61c0d463c55ceb83eff76a4f624adcac00740faca7&cur_album_id=1715134171561410565&scene=189#wechat_redirect

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。

请你找出并返回这两个正序数组的中位数。

示例 1：

• 输入：nums1 = [1,3] nums2 = [2]
• 输出：2.00000
• 解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

• 输入：nums1 = [1,2], nums2 = [3,4]
• 输出：2.50000
• 解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• 10⁶ <= nums1[i], nums2[i] <= 10⁶

（1）略解1

最简单的就使用暴力解决，合并数组后，使用 Java 自带的排序方法进行排序，然后直接取中位数即可。

这里代码为了不判断总数组的长度为奇数还是偶数，都取中间两个数然后求平均。数组长度为奇数的话，两个数都是同一个数，所以没有影响。

class Solution {
  public double findMedianSortedArrays(int[] nums1, int[] nums2) {
		// n为第一个数组的长度；m为第二个数组的长度
    int n = nums1.length, m = nums2.length;
    
    // 新建一个两个数组总长度的数组
    int[] arr = new int[n + m];
    
    int idx = 0;
    //依次放入数组中
    for (int i : nums1) arr[idx++] = i;
    for (int i : nums2) arr[idx++] = i;
    
    // 然后对总数组进行排序
    Arrays.sort(arr);
    
    // 对于长度为奇数或者偶数，都进行取两个数求平均操作
    int l = arr[(n + m) / 2], r = arr[(n + m - 1) / 2];
    return (l + r) / 2.0;
  }
}

• 时间复杂度：合并两个数组的复杂度是 O(n+m) ，对合并数组进行排序的复杂度是 O( (n+m)log(n+m) ) 。整体复杂度是 O( (n+m)log(n+m) )

但如果时间复杂度需要下降到 O( log(n+m) )，则不能再使用这个方法。

（2）略解2

第 2 种方法使用的是递归，不断缩小数组的范围，最后找到中位数。下面是该方法的步骤：

1. 找到两个数组的中位数
2. 比较两个数组的中位数，如果 A 数组的中位数大于 B 数组的中位数，则代表两个数组合并后的中位数，在 A 数组里或者 B 数组的中位数右边

第 2 点：假设一种极端的情况，A 的中位数左边全部小于 B 数组的中位数，两个数组一合并后，B 数组的原来的中位数左边数字数量一定小于右边的数量，所以新的中位数就会右移。

3. 继续在剩下的数字里找中位数

第 3 点：假设找到的总数组的中位数下标是 k，在剩余数组找中位数的时候，需要减取被剔除数字的数量，即 k - (x)。

---

具体实现如下面代码：

需要明确几个变量：

• i ：在递归中会改变，用于表示 nums1 数组的起始位置
• j ：在递归中会改变，用于表示 nums2 数组的起始位置
• k ：在递归中会改变，用于表示剩余数字里中位数在第几位置
• si ：在递归中会改变，代表当前 n1 数组的中位数下标
• sj ：在递归中会改变，代表当前 n2 数组的中位数下标
• 时间复杂度：k 从两个数组之和开始减少，每次递归 k 的规模都减少一半，复杂度为 O( log(m+n) )

public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
  // 计算出两个数组的长度
  int tot = nums1.length + nums2.length;

  // 如果总长度是偶数
  if (tot % 2 == 0) {
    // 找到第1个中位数
    int left = find(nums1, 0, nums2, 0, tot / 2);
    // 找到第2个中位数
    int right = find(nums1, 0, nums2, 0, tot / 2 + 1);
    return (left + right) / 2.0;
  } else {
    return find(nums1, 0, nums2, 0, tot / 2 + 1);
  }
}

// i代表第一个数组的起始下标；j代表第二个数组的起始下标；k代表中位数的在第几位
static int find(int[] n1, int i, int[] n2, int j, int k) {
  // n1.length - i为真实的n1长度；n2.length - j为真实的n2长度
  // 如果n1的长度大于n2的长度，则两个数组进行调换
  if (n1.length - i > n2.length - j)
    return find(n2, j, n1, i, k);
  if (i >= n1.length)
    return n2[j + k - 1];
  if (k == 1) {
    return Math.min(n1[i], n2[j]);
  } else {
    // si代表当前n1数组的中位数下标；sj代表当前n2数组的中位数下标
    int si = Math.min(i + (k / 2), n1.length), sj = j + k - (k / 2);
    // 如果n1中间的值大于n2中间的值，说明中位数在n1里面或者n2的右半部分
    // 所以继续查找，n1的起始位置不变，一样是i，n2的起始位置变成中间下标
    // k需要减取n2的左半部分
    if (n1[si - 1] > n2[sj - 1]) {
      return find(n1, i, n2, sj, k - (sj - j));
    } else {
      // 如果n1中间的值小于等于n2中间的值，同理
      return find(n1, si, n2, j, k - (si - i));
    }
  }
}

（3）详解2

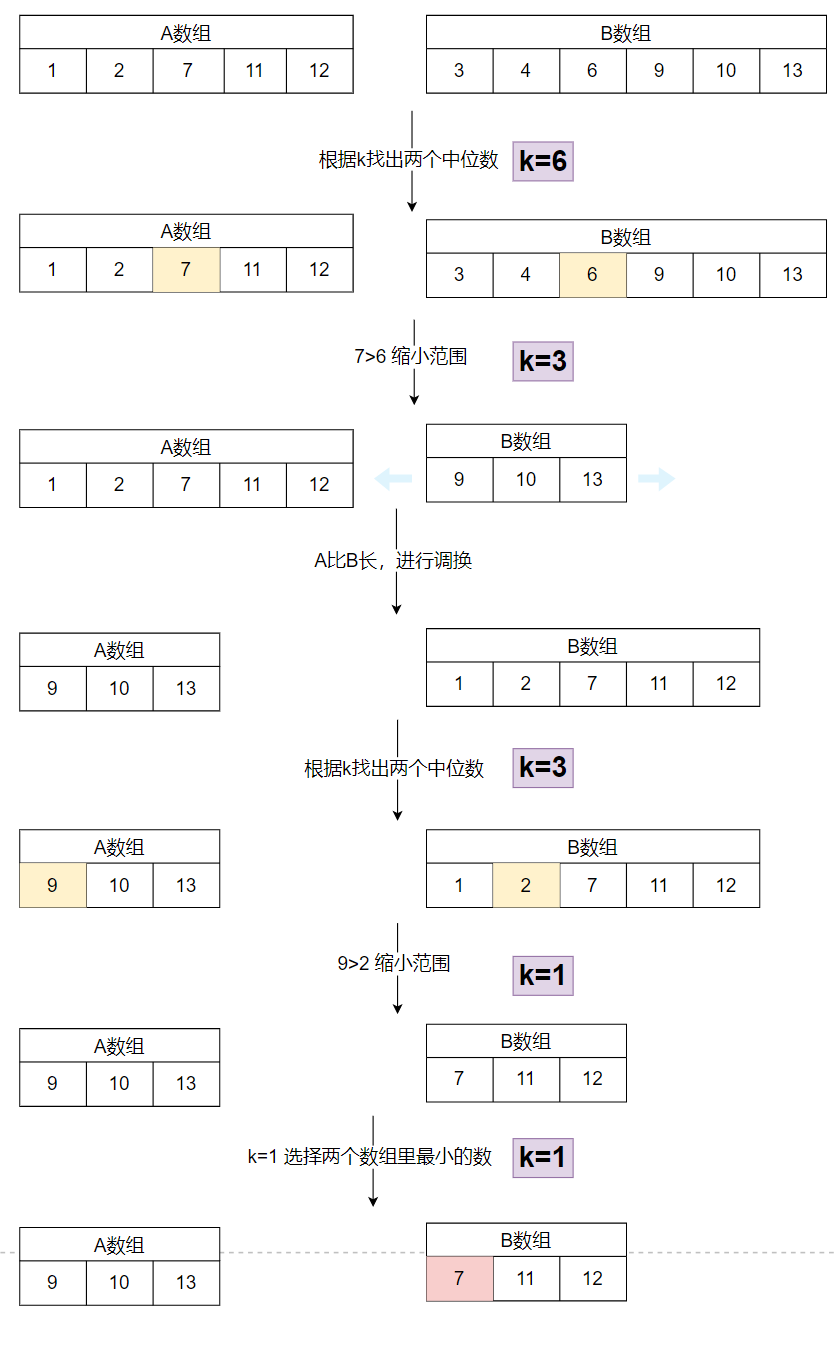
假设现在 A 数组：[ 1, 2, 7, 11, 12 ] ；B 数组：[ 3, 4, 6, 9, 10, 13 ]

• 数组总长度为 5 + 6 = 11，所以执行 find(nums1, 0, nums2, 0, 6); ，i = 0，j = 0，k = 6
• 然后比较两个数组的中位数，si = 3，sj = 3，7（n1[si-1]）> 6 （n2[sj-1]），所以中位数在 A 数组里和 B 数组的右边，现在 B 数组为 [ 9, 10, 13 ] ，k = 3 。继续执行 find(n1, 0, n2, 3, 3); ，i = 0，j = 3，k = 3
• 这时 A 数组长度大于 B 数组长度，所以进行调换。i = 3，A 数组 [ 9, 10, 13 ] ，j = 0， B 数组 [ 1, 2, 7, 11, 12 ] ，k = 3
• 然后继续比较两个数组的中位数，si = 4，sj = 2，，9（n1[si-1]）> 2（n2[sj-1]） ，所以中位数在剩余的 A 数组里和 B 数组的右边，现在 B 数组为 [ 7, 11, 12 ] ，k = 1。继续执行 find(n1, 3, n2, 2, 1);
• k = 1 ，就直接执行 Math.min(n1[i], n2[j]); ，这句代码的意思就是在两个剩余数组中找第 1 小的数，A 数组中最小数为 9 ，B 数组中最小数为 7，所以中位数为 7 。

图片版：

（4）总结

第 2 个方法核心是不断地找 一定不是中位数的数，例如第 1 次比较，就排除了 B 数组里的一半，然后依次类推，直到排除数字的数量足够。

六、找出不含重复字符的最长子串

原题链接：https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=6&sn=6a6fd8a208ccd7f0b7d706a3ff5900d7&chksm=fd9ca9fdcaeb20eb43980e8c841294d8b366fdbc128dacf140a93740221691ba241fe4593501&cur_album_id=1715134171561410565&scene=189#wechat_redirect

给定一个字符串，请你找出其中不含有重复字符的「最长子串」的长度。

示例 1:

• 输入: s = "abcabcbb"
• 输出: 3
• 解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3

示例 2:

• 输入: s = "bbbbb"
• 输出: 1
• 解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1

提示：

• 0 <= s.length <= 5 * 10⁴
• s 由英文字母、数字、符号和空格组成

（1）略解1

题目要求的是子串，所以可以设置两个指针，分别指向子串的头和尾。

因为需要无重复字符，所以当尾指针往后移动时，需要查看当前子串是否有重复字符。如果有重复字符，就需要将头指针向后移动，直到无重复字符。

为什么要移动头指针，因为移动头指针一定会消除子串的重复字符。这种方法称为滑动窗口。

这时需要用到 Java 里的哈希表来得知当前子串是否有重复字符。我们需要使用到哈希表的三个方法：

• map.getOrDefault(key, 0) ：参数 1 是 key 值，参数 2 是没有找到 key 时的默认 value 值。获取指定 key 的 value 值
• map.get(key) ：与上面的作用一致，只是不会返回默认值
• map.put(key, value) ：将 key 和 value 放入哈希表中。

具体代码如下

public int lengthOfLongestSubstring(String s) {
  // 创建一个key为字符类型，value为整性类型的哈希表
  Map<Character, Integer> map = new HashMap<>();
  
  int ans = 0;
  // i为头指针，j为尾指针
  for (int i = 0, j = 0; j < s.length(); j++) {
    // 取出j所指向的字符
    char r = s.charAt(j);
    
    // 将字符存入哈希表中 
    map.put(r, map.getOrDefault(r, 0) + 1);
    
    // 判断当前字符是否重复
    while (map.get(r) > 1) {
      // 取出i所指向的字符
      char l = s.charAt(i);
      // 将重复的字符去掉，即该字符的数量减1
      map.put(l, map.get(l) - 1);
      // 将i头指针向后移动
      i++;
    }
    
    // 将当前没有重复字符子串的长度记录
    ans = Math.max(ans, j - i + 1);
  }
  return ans;
}

（2）详解1

假设现在有一个字符：ewqrtewdrtyrit （瞎打的），请找出这个字符不含重复字符的最长子串的长度。

• 第 1 个记录的子串是：ewqrt ，其长度为 5
• 尾指针向右移动一位，然后遇到了重复字符 e ，所以头指针向右移动一位，第 2 个记录的子串为：wqrte ，其长度为 5
• 尾指针向右移动一位，然后遇到了重复字符 w，所以头指针向右移动一位，第 3 个记录的子串为：qrtew ，其长度为 5
• 尾指针向右移动一位，没有重复字符，第 4 个记录的子串 qrtewd ，其长度为 6
• 尾指针向右移动一位，然后遇到了重复字符 r，所以头指针向右移动两位，第 5 个记录的子串 tewdr ，其长度为 5
• 尾指针向右移动一位，然后遇到了重复字符 t，所以头指针向右移动一位，第 6 个记录的子串 ewdrt，其长度为 5
• 尾指针向右移动一位，没有重复字符，第 7 个记录的子串 ewdrty ，其长度为 6
• 尾指针向右移动一位，然后遇到了重复字符 r，所以头指针向右移动四位，第 8 个记录的子串为 tyr，其长度为 3
• 尾指针向右移动一位，没有重复字符，第 9 个记录的子串 tyri ，其长度为 4
• 尾指针向右移动一位，然后遇到了重复字符 t，所以头指针向右移动一位，第 10 个记录的子串 yrit ，其长度为 4
• 所以不含重复字符的最长子串是 qrtewd 和 ewdrty ，长度为 6

七、两数相加

原题链接：https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=7&sn=af1309aebca76e2a70ed93b1a8f57e20&chksm=fd9ca9fdcaeb20eb9b5ffcdb3af2e7f279bf876225117804538f3a896b92e9e9fa49ac708415&cur_album_id=1715134171561410565&scene=189#wechat_redirect

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

示例 1：

• 输入：l1 = [2,4,3]， l2 = [5,6,4]

• 输出：[7,0,8]

• 解释：342 + 465 = 807

示例 2：

输入：l1 = [0]， l2 = [0]

输出：[0]

提示：

• 每个链表中的节点数在范围 [1, 100] 内
• 0 <= Node.val <= 9
• 题目数据保证列表表示的数字不含前导零

（1）略解

这道题是模拟题，模拟人工竖式做加法的过程，这里需要用到链表，因为 Java 里没有自带链表类型，所以需要自己定义链表类。

链表类需要三个东西：

• 构造方法，初始化当前节点的值
• val 属性，其类型为整型，存放需要相加的数字
• next 属性，其类型为 ListNode ，用于指向下一个链表

public class ListNode {
  int val;
  ListNode next;
  ListNode(int x) { val = x; }
}

然后具体代码，就是让两数相加，然后用一个变量代表进位的数，用一个变量不断移动来扩展链表。

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
  // 答案所存放的链表
  ListNode dummy = new ListNode(0);
  // 用来扩展链表的尾指针
  ListNode tmp = dummy;
  // 存放进位的数
  int t = 0;
  
  while (l1 != null || l2 != null) {
    // 如果l1或者l2为空，代表当前位置没有数字，则初始化为零
    int a = l1 != null ? l1.val : 0;
    int b = l2 != null ? l2.val : 0;
    
    // 将加起来的数临时存放到变量t里
    t = a + b + t;
    // 尾指针的下一个数是变量t的个位数
    tmp.next = new ListNode(t % 10);
    // 将变量t除以10，变回
    t /= 10;
    // 尾指针移动下一个节点
    tmp = tmp.next;
    
    // 如果当前节点不为空，则代表下一位一定有数字
    if (l1 != null) l1 = l1.next;
    if (l2 != null) l2 = l2.next;
  }
  
  // 如果退出循环后依然有进位，则再新建一个节点
  if (t > 0) tmp.next = new ListNode(t);
  
  // 最后返回去掉虚拟头节点的链表
  return dummy.next;
}

（2）虚拟头节点

做有关链表的题目，有个常用技巧：添加一个虚拟头结点（哨兵），帮助简化边界情况的判断，例如第 1 次进入方法时。

第 1 次进入方法，如果没有设置虚拟头节点，则要额外单独计算第 1 位的值。因为两个数组至少有 1 个节点，所以计算第 1 位的值不需要判空。

可见下面代码，额外计算第 1 位的值，会产生很多相同代码，但因为需要第 5 行的初始化，所以不能省略。如果添加一个虚拟头节点，第 1 位就是 0，不用计算就能得出，然后真实的第 1 位就可以在循环中计算。

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
  // 额外的单独计算第 1 位的值
  int t = 0;
  t = l1.val + 12.val;
  ListNode dummy = new ListNode(t);
  ListNode tmp = dummy;
  t /= 10;
  tmp = tmp.next;
  l1 = l1.next;
  l2 = l2.next;
  
  while (l1 != null || l2 != null) {
    int a = l1 != null ? l1.val : 0;
    int b = l2 != null ? l2.val : 0;
    t = a + b + t;
    tmp.next = new ListNode(t % 10);
    t /= 10;
    tmp = tmp.next;
    if (l1 != null) l1 = l1.next;
    if (l2 != null) l2 = l2.next;
  }
  if (t > 0) tmp.next = new ListNode(t);
  
  // 更改返回的值
  return dummy;
}

• 时间复杂度：m 和 n 分别代表两条链表的长度，则遍历到的最远位置为 max(m,n)， 复杂度为 O( max(m,n) )
• 空间复杂度：创建了 max(m,n) + 1 个节点（含哨兵），复杂度为 O( max(m,n) )

该文档完成时间： 2022年6月24日