算法二-7月11
算法二-7月11
八、两数之和
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484130&idx=8&sn=31e3191597de49983f9db37aae074e8c&chksm=fd9ca9fdcaeb20eba4699df2cd7d411bc4a29b4f21493de371c97c507b711489695dd8d3ddc7&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值的那两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
你可以按任意顺序返回答案。
示例 1:
- 输入:nums = [2,7,11,15], target = 9
- 输出:[0,1]
- 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
- 输入:nums = [3,2,4], target = 6
- 输出:[1,2]
提示:
- 2 <= nums.length <= 103
- -109 <= nums[i] <= 109
- -109 <= nums[i] <= 109
- 只会存在一个有效答案
(1)略解1
最简单的方法就是两层循环进行遍历,需要注意的是 i 和 j 的取值,i 取值 [ 0,n-1 ] ,j 取值 [ i+1,n ] ,这样可以防止取到重复解
public int[] twoSum(int[] nums, int t) {
int n = nums.length;
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) {
if (t == nums[i] + nums[j]) return new int[]{i,j};
}
}
return new int[]{};
}
- 时间复杂度:两重循环,复杂度为 O( n2 )
- 空间复杂度:O(1)
(2)略解2
首先,任何优化的思路都是 “ 减少重复 ”。
从朴素解法中可以知道,逻辑上我们是先定下来一个数,然后从数组中往后找另外一个值是否存在。
然后我们找第二个数的过程中是重复扫描了数组多次,我们如果能使用到第 1 次所扫描的结果,会可以简化复杂度。判断一个数是否已经存在,直观感受就是使用哈希表。
思路:
- 首先先将所有数字存放到哈希表中
- 然后循环每一个数,计算出第 2 个数的值,然后在哈希表中查找
- 查找之前,需要判断当前的第 1 个数是否在哈希表中,如果在的话就要删除
注意:因为每次哈希表存放相同元素时,新值会覆盖旧值,所以哈希表中存放的都是相对较后面的下标
public int[] twoSum(int[] nums, int t) {
Map<Integer, Integer> map = new HashMap<>();
// 初始化哈希表,key值为数组中的数,value值为数字所在数组的下标
for (int i = 0; i < nums.length; i++) map.put(nums[i], i);
for (int i = 0; i < nums.length; i++) {
// a代表数组中的数,b代表所需要的第2个数
int a = nums[i], b = t - a;
// 如果哈希表中存在当前的数字,则删除
if (map.get(a) == i) map.remove(a);
// 然后在哈希表中查找所需要的第2个数
if (map.containsKey(b)) return new int[]{i, map.get(b)};
}
return new int[]{};
}
最坏情况下,每个数会对应一次哈希表的插入和删除。 例如数组中没有相同的元素,哈希表都存放的是第 1 个数的下标,每次都要删除。
- 时间复杂度:会扫描数组两次,复杂度是 O( n ) (忽略常数)
- 空间复杂度:使用了哈希表进行记录,复杂度是 O ( n )s
(3)略解3
这时候不妨将思路逆转过来,遍历过程中指定第二个数,使用哈希表在第二个数的前面去找第一个数。一边加入哈希表,一边找需要的数。
因为最后都会遍历完整个数组,所以不担心会少数字。
class Solution {
public int[] twoSum(int[] nums, int t) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
// a代表数组中的数,b代表所需要的第2个数
int a = nums[i], b = t - a;
// 判断哈希表中是否有b所代表的数字
if (map.containsKey(b)) return new int[]{map.get(b), i};
// 将数组中的数放入哈希表中
map.put(a, i);
}
return new int[]{};
}
}
- 时间复杂度:会扫描数组一次,复杂度是 O( n ) (忽略常数)
- 空间复杂度:使用了哈希表进行记录,复杂度是 O ( n )
- 虽然第 2 种和第 3 种的复杂度一致,但第 3 种思路依然很完美
总结:初始化是一个比较讲究的操作,结合题目自定义初始化,会少了很多麻烦。
这道题将初始化和比较结合在了一起。上一道题设置虚拟头节点,将初始化放入到循环中去。
九、最长回文子串
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484229&idx=6&sn=7b8c5e69f04f0b86616300bd3761c75d&chksm=fd9ca85acaeb214cb2b47c277dd79245edba39f5d7be9eafe634768c6586ce620aa776edd850&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
- 输入:s = "babad"
- 输出:"bab"
- 解释:"aba" 同样是符合题意的答案
示例 2:
- 输入:s = "cbbd"
- 输出:"bb"
提示:
- 1 <= s.length <= 1000
- s 仅由数字和英文字母(大写和/或小写)组成
(1)略解1
这道题类似于第 6 题,也是找出符合条件的子串,但这道题不能使用滑动窗口来解决,因为回文串这个条件不好判断。
首先还是先使用暴力方法解决,循环遍历每个字符,作为回文串的中心,然后向左右扩展比较。
- 回文串长度是奇数,中心是字符串的某个字符——s[i],则判断 s[i − k] == s[i + k], k = 1,2,3 ……
- 回文串长度是偶数,中心是两个字符的中间,假设—— s[i] 是中心,则判断前一个字符和 s[i] ,
s[i − k] == s[i + k − 1], k = 1,2,3…
public String longestPalindrome(String s) {
String ans = "";
for (int i = 0; i < s.length(); i++) {
// 回文串为奇数
if (s.length() % 2 == 1) {
int l = i - 1, r = i + 1;
// 获取当前中心的最长回文串
String sub = getString(s, l, r);
// 如果当前回文串的值大于之前的值,则进行替换
if (sub.length() > ans.length()) ans = sub;
} else {
// 回文串为偶数
l = i - 1;
r = i + 1 - 1;
sub = getString(s, l, r);
if (sub.length() > ans.length()) ans = sub;
}
}
return ans;
}
// 获取当前中心的最长回文串
String getString(String s, int l, int r) {
// 如果左右边界没有超出数组,并且比较的字符相等,则继续比较
while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
return s.substring(l + 1, r);
}
- 时间复杂度:先枚举了
s中的每个字符作为回文串的中心点,再从中心点出发左右扩展,最多扩展到边界。复杂度是 O ( n2 ) - 空间复杂度:O (1)
(2)略解2
有一个算法叫 Manacher 算法,其可以将时间复杂度降到 O ( n ),其用来解决 “ 回文串 ” 问题。算法比较复杂,有很多步:
参考链接:
- https://youtu.be/kbUiR5YWUpQ
- https://www.cnblogs.com/cloudplankroader/p/10988844.html
第 1 步:处理字符串
- 操作:将字符串的所有间隔插入 “ # ” 符号,例如 “ abaabc ” ,处理完后就变成 “ #a#b#a#a#b#c ”
- 原因:为了处理原来字符串长度的奇偶问题,处理完后一定是奇数。
- 证明:“ aa ” => " #a#a# " ,长度 2 => 长度 5;“ a ” => " #a# ",长度 1 => 长度 3
第 2 步:声明变量
需要说明几个变量的作用:
- R:最长回文串的右边界。不会经常变动,除非有新右边界超过了当前边界。
- C:最长回文串的中心。不会经常变动,除非 R 更新了。也就是说 R 和 C 会同时更新
- L:最长回文串的右边界关于 C 的对称。
- i :循环到的字符的下标
- i' :循环到的字符关于 C 的对称的下标
- pArray:数组,每个回文串的半径长度
第 3 步:声明情况
i 循环的时候会遇到几种情况,操作都不同:
- i > R :暴力匹配,然后看下是否要更新 R、C、L 变量
- i <= R :获取到 i' 的值,因为 i' 和 i 是对称的,所以 i' 和 i 的回文情况是一样的。但需要继续看 i' 的值赋值给 i 后,是否超出了 R 的值。
- (i' 的位置是 2 * C - i,推导 i' = R - i + L,因为 R = L + (C - L)*2,所以 i' = L + (C - L)*2 - i + L = 2C - i)
- 如果没有超出 R 的值,则直接取 i' 的值
- 如果超出了,就只能取 i 到 R 的这个范围的回文串
- 如果等于 R 的值,则继续在 i' 的基础上继续扩展
可以证明上面三种情况:
- 没有超出 R 的值,证明 i 的回文情况和 i' 的完全一致,所以可以直接取 i' 的值。和 KMP 算法类似
- 超出了 R 的值,假设 R 的右边是变量 b,关于 i 的对称 R' 的左边是变量 a,L 的左边是变量 x,关于 i' 对称的 L' 的右边是变量 y。
因为 i' 的回文串长度是超过 L 的,x 等于 y。因为关于 C 对称关系,y 又等于 a。但因为 R 是最长回文串的边界,所以 x 不等于 b。最后等于 y 不等于 b,所以 i 为中心的回文串最多到 R 处。
- 如果等于 R 的值,无法得知 L 的左边和 R 的右边的关系,所以需要继续扩展。
下面图片比较清楚:
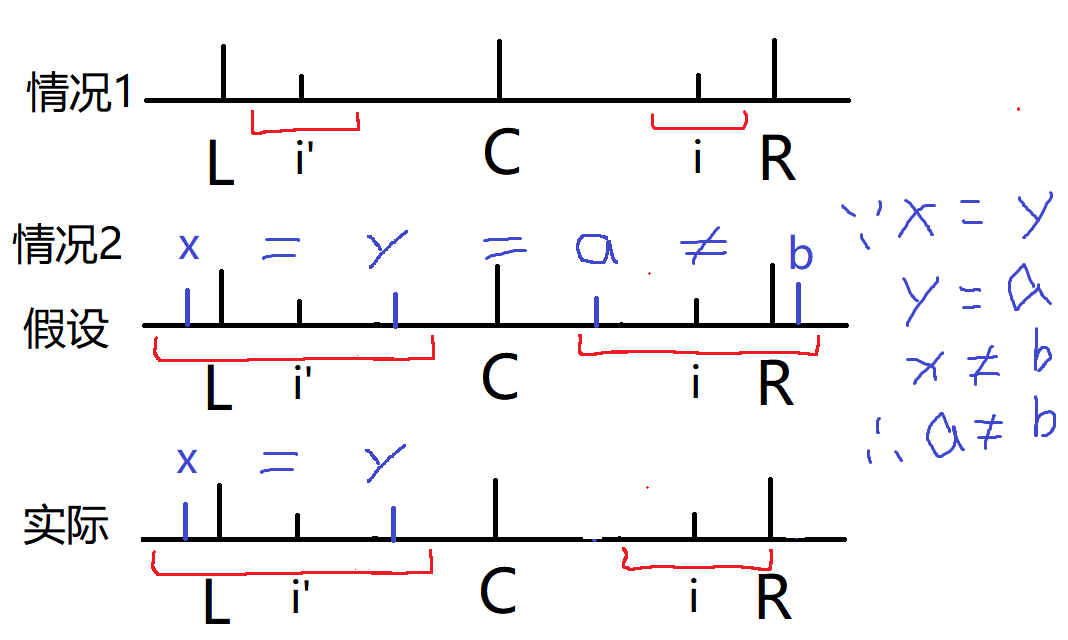
第 4 步:继续循环不断地移动 i
下面为全部代码:为了简化代码,不只第 3 种情况(i 的值与 i 到 R 的距离一致)进行扩展搜索。
public String longestPalindrome(String s) {
if (s.length() == 1) return s;
// 处理字符串
char[] chars = manacherString(s);
// n代表新字符串长度
int n = chars.length;
// pArr存放每个字符的最长回文串长度
int[] pArr = new int[n];
// 初始化C,R,和最长回文串的中心pos
int C = -1, R = -1, pos = -1;
// 将最大值初始化为整型的最小值
int max = Integer.MIN_VALUE;
// 遍历每一次字符
for (int i = 0; i < n; i++) {
// 判断i是否小于R,如果小于则在取i'的值与i到右边界的距离比较,取最小值
pArr[i] = i < R ? Math.min(pArr[C * 2 - i], R - i) : 1;的
// 然后i'的值的基础上继续扩展
while (i + pArr[i] < n && i - pArr[i] > -1) {
if (chars[i + pArr[i]] == chars[i - pArr[i]]) {
pArr[i]++;
} else {
break;
}
}
// 如果i的右边界大于R,则更新R和C
if (i + pArr[i] > R) {
R = i + pArr[i];
C = i;
}
// 判断当前回文串的长度是否为最大
if (pArr[i] > max) {
max = pArr[i];
pos = i;
}
}
// 取出最长的半径长度
int offset = pArr[pos];
// 将字符串还原
StringBuilder sb = new StringBuilder();
for (int i = pos - offset + 1; i <= pos + offset - 1; i++) {
if (chars[i] != '#') sb.append(chars[i]);
}
return sb.toString();
}
// 往字符串加入#符号的方法
char[] manacherString(String s) {
char[] chars = new char[s.length() * 2 + 1];
for (int i = 0, idx = 0; i < chars.length; i++) {
chars[i] = (i & 1) == 0 ? '#' : s.charAt(idx++);
}
return chars;
}
(3)详解2
假设现在有一个字符串 " abaabc " ,进行字符串处理后 “ #a#b#a#a#b#c# ”
- 现在先遍历第 1 个字符,i = 0,R = -1,C = -1。i > R,所以对于第 1 个 # 为中心,搜索回文串。没有搜索任何字符就遇到了字符串边界,所以回文半径为 1,即 pArray[1] = 1。然后更新 R 和 C,C = 0;这里将 R 指向右边界的下一个字符,便于操作,所以 R = 1
- 然后遍历第 2 个字符,i = 1,R = 1,C = 0。i = R,但关于 C 对称无字符,所以直接搜索回文串。搜索了 “ #a# ”,所以回文半径为 3,pArray[1] = 3。R = 3,C = 1
- 然后遍历第 3 个字符,i = 2,R = 3,C = 1。i < R,看 pArray[i'] 的值,i' = 0,pArray[0] = 1;然后看与 R 的距离,R - i = 3 - 2 = 1,所以去哪个都行,pArray[2] = 1
- 然后遍历第 4 个字符,i = 3,R = 3,C = 1。i = R,但关于 C 对称无字符,所以直接搜索回文串。搜索了 “ #a#b#a# ”,所以回文半径为 4,pArray[3] = 4。R = 7,C = 3
- 然后遍历第 5 个字符,i = 4,R = 7,C = 3。i < R,看 pArray[i'] 的值,i' = 2,pArray[2] = 1;然后看与 R 的距离,R - i = 7 - 4 = 3,所以取最小值,pArray[4] = 1
十、 整数反转
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484229&idx=5&sn=6884cd97b248c71e8be57ebc5d68596e&chksm=fd9ca85acaeb214c2387dad51736521c846d6daf036bb9db95f300ffbb8b14b578e92fa6628e&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
注意:
假设我们的环境只能存储得下 32 位的有符号整数,则其数值范围为 [ -2-31, 231− 1 ]。
请根据这个假设,如果反转后整数溢出那么就返回 0
(1)略解1
这道题在第 3 题的时候已经有相关思路了,就是如何判断当前整数溢出的思路。这次需要分别判断负数和正数
如果是正数,原来
ans * 10 + x % 10 > Integer.MAX_VALUE,变为ans > (Integer.MAX_VALUE - x % 10) / 10如果是负数,原来
ans * 10 - x % 10 < Integer.MIN_VALUE,变为ans * 10 > (Integer.MIN_VALUE + x % 10) / 10
然后就不断循环遍历每一个数就可以了。其中反转意思就是,将原始的数字从个位开始进栈,所以从第 1 次循环开始,答案右移并加上个位数
public int reverse(int x) {
int ans = 0;
while (x != 0) {
// x为正数的判溢出条件
if (x > 0 && ans > (Integer.MAX_VALUE - x % 10) / 10) return 0;
// x为负数的判溢出条件
if (x < 0 && ans < (Integer.MIN_VALUE - x % 10) / 10) return 0;
// 答案右移一位,再加上个位数
ans = ans * 10 + x % 10;
// 将已经加上的数去掉
x /= 10;
}
return ans;
}
时间复杂度:数字 x 的位数大约有 lg x 位(10位数 ≈ x )。复杂度为 O ( lg x )
空间复杂度:O ( 1 )
十一、数字转罗马数字
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484229&idx=4&sn=5f096dbcd6d5d915f7ac0cfcaa99f8a1&chksm=fd9ca85acaeb214cb5004edc947177a80b59df11861c5fcc61814c47c527949d285b65818545&cur_album_id=1715134171561410565&scene=189#wechat_redirect
罗马数字包含以下七种字符:I(1), V(5), X(10), L(50),C(100),D(500) 和 M(100)。
通常情况下,罗马数字中小的数字在大的数字的右边,表示加法。 如果小的数字在大的数字的左边,表示减法,但只有六种情况。
- I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
- X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
- C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个整数,将其转为罗马数字。输入确保在 1 到 3999 的范围内。
示例 1 :
- 输入: 58
- 输出: " LVIII "
- 解释: L = 50, V = 5, III = 3.
示例 2:
- 输入: 1994
- 输出: " MCMXCIV "
- 解释: M = 1000, CM = 900, XC = 90, IV = 4.
(1)略解1
这道题有点简单,使用贪心算法即可,类似于经典的背包问题,每次装单位体积价值最大的物品。这里是每次看当前位数最接近哪个罗马数字。
// 按大小排列罗马数字所代表的值
int[] val = new int[]{1000,900,500,400,100,90,50,40,10,9,5,4,1};
// 将罗马数字与上面的数组对齐
String[] str = new String[]{"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
public String intToRoman(int x) {
// 存放罗马数字
StringBuilder sb = new StringBuilder();
// 退出循环条件有两个:
// 1. 主要条件是x>0,如果x被减完了当然就要退出循环
// 2. 另一个条件只是习惯写法,因为下面代码要取数组的值,
// 但x>0时,i永远不会超过数组的长度,所以不加上也可以
for (int i = 0; i < val.length && x > 0; i++) {
// 取出罗马数字所代表的值
int cv = val[i];
// 取出罗马数字
String cs = str[i];
// 如果当前的输入值大于罗马数字,则继续循环减取罗马数字的值
while (x >= cv) {
// 最终结果不断添加罗马数字
sb.append(cs);
// 输入值不断减少
x -= cv;
}
}
return sb.toString();
}
- 时间复杂度:计算量与最终罗马数字的长度成正比。对于每一位阿拉伯数字,罗马数字最多用 4 个字母表示。
例如个位数,最大的单个罗马数字是 9,其次是 5、1。9 对于 5 和 5 对于 1,都差距 4,理论上 8(VIII),4(IIII),但由于有罗马数字 4(IV),所以最多差距 VIII,则罗马数字的长度最多不超过阿拉伯数字长度的 4 倍。阿拉伯数字的长度约为 lgn ,因此罗马数字的长度不超过 4 * lgn 。复杂度为 O(lgn)
- 空间复杂度:虽然使用了两个数组记录罗马字符和数值,但消耗的空间固定,不随着样本大小而变化。复杂度为 O(1)
十二、最长公共前缀
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484229&idx=3&sn=6a5fe467fc450b397c67f8ae45d4d2b7&chksm=fd9ca85acaeb214c8b4993324b4faded8f6724d18849273f07065253faef31c3bba834bb4e59&cur_album_id=1715134171561410565&scene=189#wechat_redirect
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
- 输入:strs = ["flower","flow","flight"]
- 输出:"fl"
示例 2:
- 输入:strs = ["dog","racecar","car"]
- 输出:""解释:输入不存在公共前缀。
提示:
- 0 <= strs.length <= 200
- 0 <= strs[i].length <= 200
- strs[i] 仅由小写英文字母组成
(1)略解1
public String longestCommonPrefix(String[] ss) {
String ans = "";
// 如果数组为空则直接返回空字符串
if (ss.length == 0) return ans;
// 这个循环用于取出字符串的每个字符
for (int i = 0; i < Integer.MAX_VALUE; i++) {
// 取出第1个字符串
String s = ss[0];
// 如果当前的i已经超过第1字符串的长度,
// 证明最长公共前缀不会继续增加了,直接返回结果
if (i >= s.length()) return ans;
// 取出某个字符
char c = ss[0].charAt(i);
// 再对字符串数组进行遍历
for (String item : ss) {
// 如果当前的i超过某个字符串的长度,或者取出的字符不相等,
// 则直接返回结果
if (i >= item.length() || item.charAt(i) != c) return ans;
}
// 能到这行证明当前字符每个字符串都有,所以添加到结果里
ans += String.valueOf(c);
}
return ans;
}
说明:判断条件不一定要写成 i < Integer.MAX_VALUE,题目给出了范围是 200 以内,写成 i <= 200 也可以。不影响执行效率。
时间复杂度:对于 n 个字符串,都需要遍历到公共前缀长度 m。复杂度为 O (nm)
空间复杂度:需要存储公共前缀作为答案返回。复杂度为 O (m)
总结:这道题写了我快一个小时,主要还是思路不够明确。
- 要明确需要的数据,这道题需要的是字符串;
- 明确循环的目的,这道题第 1 个循环遍历字符串,第 2 个循环遍历数组;
- 明确数据更新的条件,这道题是当有字符不相等,或者该位置的字符不存在。
- 最后注意一下边界问题,这道题是
string.charAt()方法的边界问题。
十三、盛最多水的容器
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484229&idx=2&sn=e3d730a608987d3c764f17578ab4e8af&chksm=fd9ca85acaeb214cb2ab0e66b3ee5f8b20a5159aef56e23b92669669b039187836d53ce48bb7&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给你
n个非负整数a1,a2,...,an,每个数代表坐标中的一个点(i, ai)。在坐标内画
n条垂直线,垂直线i的两个端点分别为(i, ai)和(i, 0)。找出其中的两条线,使得它们与
x轴共同构成的容器可以容纳最多的水。示例 1:
- 输入:[1,8,6,2,5,4,8,3,7]
- 输出:49
- 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
- 输入:height = [1,1]
- 输出:1
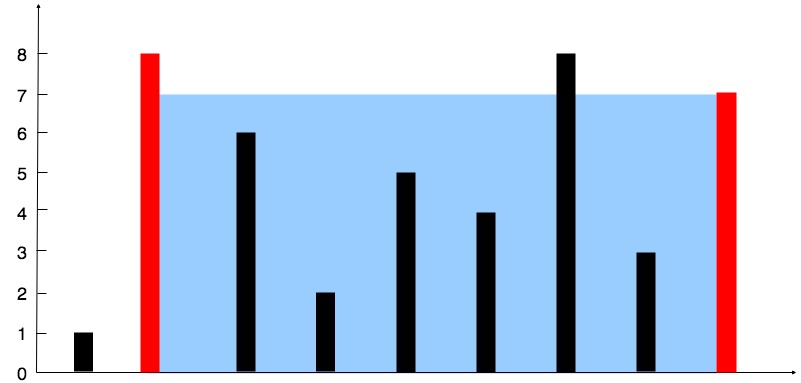
提示:
- n = height.length
- 2 <= n <= 3 * 104
- 0 <= height[i] <= 3 * 104
(1)略解1
首先是暴力解法,暴力解法就是一个一个遍历,然后计算每个面积,选出那个最大的面积。
public int maxArea(int[] height) {
int n = height.length;
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int w = j - i;
int h = Math.min(height[i], height[j]);
ans = Math.max(w * h, ans);
}
}
return ans;
}
(2)略解2
第 2 个解法:双指针 + 贪心解法
左右指针 i 、j 都指向一个数,然后向中间移动。w 为 i、j 的距离,代表矩形的底;然后 i 、j 所指向的数字,最小的为矩形的高 h。
首先考虑两种情况:
- 移动高的指针:w 一定变小
- 移动后的数字比之前小,h 可能变小,因为 w 一定变小,所以 面积一定变小。
- 移动后的数字比之前相等,因为 w 变小,所以 面积变小。
- 移动后的数字比之前大,h 不变(木桶效应),因为 w 变小,所以 面积变小。
- 总结:不能移动两个指针较高的
- 移动低的指针:w 一定变小
- 移动后的数字比之前小,h 一定变小,再加上 w 变小,所以 面积一定变小。
- 移动后的数字比之前相等,h 不变,w 一定变小,所以 面积一定变小。
- 移动后的数字比之前大,h 变大,但 w 变小,所以 面积可能变大。
- 但是否符合贪心选择性质?
- 贪心选择性质: 一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。
- 两个指针一个在开头,一个在结尾,如果需要移动指针来找比初始的大的面积,就一定只能移动高度较低的,否则不可能比初始的大。当移动后无论面积是增加还是减少,只能不断移动高度较低的,才有可能找到比现在大的值。所以每次只根据当前的指针的高度来移动,符合局部最优解。
public int maxArea(int[] height) {
int n = height.length;
// 初始化两个指针
int i = 0, j = n - 1;
int ans = 0;
// 当i=j时就可以退出循环了
while (i < j) {
// 判断当前的面积是否大于已记录的答案
ans = Math.max(ans, (j - i) * Math.min(height[i], height[j]));
// 根据高度移动不同的指针
if (height[i] < height[j]) {
i++;
} else {
j--;
}
}
return ans;
}
- 时间复杂度:会对整个数组扫描一遍。复杂度为 O ( n )
- 空间复杂度:O (1)
十四、绝对差不超过限制的最长连续子数组
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484403&idx=1&sn=9311c773c488d8b9573e5b0e3be9445e&chksm=fd9ca8eccaeb21fa5d1febd26cef4d4fe94e6600f5d2426d9cad43012a94c409d44c0bd2b5ec&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1:
- 输入:nums = [8,2,4,7], limit = 4
- 输出:2
- 解释:所有子数组如下:
- [8] 最大绝对差 |8-8| = 0 <= 4.
- [8,2] 最大绝对差 |8-2| = 6 > 4.
- [8,2,4] 最大绝对差 |8-2| = 6 > 4.
- [8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
- [2] 最大绝对差 |2-2| = 0 <= 4.
- [2,4] 最大绝对差 |2-4| = 2 <= 4.
- [2,4,7] 最大绝对差 |2-7| = 5 > 4.
- [4] 最大绝对差 |4-4| = 0 <= 4.
- [4,7] 最大绝对差 |4-7| = 3 <= 4.
- [7] 最大绝对差 |7-7| = 0 <= 4.
- 因此,满足题意的最长子数组的长度为 2 。
提示:
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^9
- 0 <= limit <= 10^9
(1)二分解法
对数解法就是二分法。
二分的是结果数组的长度,如果结果数组的长度超过原数组的一半,则长度继续扩大,否则长度减少。
- 变量 r 代表结果数组长度
- 变量 mid 代表数组长度的一半
check()方法检测被分成两部分的数组是否符合题目条件(数组里的绝对差不超过限制)。如果超过了,则将变量 l 变大,使数组长度边长;否则将 r 变小,使数组长度变小。
public int longestSubarray(int[] nums, int limit) {
int n = nums.length;
int l = 1, r = n;
while (l < r) {
// 计算中间的数的下标
int mid = l + r + 1 >> 1;
if (check(nums, mid, limit)) {
// 将mid赋值给l,使l变大
l = mid;
} else {
// 将mid-1赋值给r,使r变小
r = mid - 1;
}
}
return r;
}
主要还是看 check() 方法的实现方式:分别创建两个队列,然后找出顺序和逆序的子序列,然后比较顺序的第 1 个元素和逆序的第 1 个元素。
- 第 3 行:使用到是 Deque 单调队列,用于存放顺序(
Min)和逆序(Max)子序列,里面存放的是下标。 - 第 4 行:循环的起始条件是
r = 0,l = r - len + 1,这个模仿队列一个元素一个元素加进去,即 r ——最右边的下标从 0 开始。 - 第 5 ~ 7 行:
max.peekFirst() < l,其实是判断顺序和逆序的队列是否在变量 l 之后,如果在 l 之后,下标一定会大于 l。小于的话,就是队列的第 1 个下标不应该在队列里,则去掉第 1 个字符。 - 第 8 ~ 11 行:
nums[r] >= nums[max.peekLast()],其实就是判断当前的数字是否大于逆序的最后一个字符,如果大于则去掉最后一个字符,再继续判断,直到可以将当前数字逆序放进队列。 - 下面代码就是和逆序相似的操作。
- 第 21 ~ 23 行:
Math.abs(nums[max.peekFirst()] - nums[min.peekFirst()]) <= limit,就是判断最大绝对差是否符合条件。l >= 0的条件为的是让当前的队列符合长度再进行判断。
boolean check(int[] nums, int len, int limit) {
int n = nums.length;
Deque<Integer> max = new ArrayDeque<>(), min = new ArrayDeque<>();
for (int r = 0, l = r - len + 1; r < n; r++, l = r - len + 1) {
if (!max.isEmpty() && max.peekFirst() < l) {
max.pollFirst();
}
while (!max.isEmpty() && nums[r] >= nums[max.peekLast()]) {
max.pollLast();
}
max.addLast(r);
if (!min.isEmpty() && min.peekFirst() < l) {
min.pollFirst();
}
while (!min.isEmpty() && nums[r] <= nums[min.peekLast()]) {
min.pollLast();
}
min.addLast(r);
if (l >= 0 && Math.abs(nums[max.peekFirst()] - nums[min.peekFirst()]) <= limit) {
return true;
}
}
return false;
}
- 时间复杂度:不断取中间的复杂度为 O(logn) ,对于每次
check而言,每个元素最多入队和出队常数次,复杂度为 O( n ) 。整体复杂度为 O ( nlogn ) - 空间复杂度:O( n )
(2)双指针解法
事实上我们可以直接使用 双指针解法 找到最大值。始终让右端点 r 右移,当不满足条件时让 l 进行右移。
同时,还是使用 单调队列 保存我们的区间最值,这样我们只需要对数组进行一次扫描即可得到答案。不然在移动指针的时候,如果移出了最小值,则需要重新在当前数组中找出最小。
public int longestSubarray(int[] nums, int limit) {
int n = nums.length;
int ans = 0;
Deque<Integer> max = new ArrayDeque<>(), min = new ArrayDeque<>();
for (int r = 0, l = 0; r < n; r++) {
// 将当前的数字放入逆序队列
while (!max.isEmpty() && nums[r] >= nums[max.peekLast()]) {
max.pollLast();
}
max.addLast(r);
// 将当前的数字放入顺序队列
while (!min.isEmpty() && nums[r] <= nums[min.peekLast()]) {
min.pollLast();
}
min.addLast(r);
// 判断绝对差是否大于限制
while (Math.abs(nums[max.peekFirst()] - nums[min.peekFirst()]) > limit) {
// 大于的话,移动左边的指针
l++;
// 查找当前指针是否存在两个队列里
if (max.peekFirst() < l) max.pollFirst();
if (min.peekFirst() < l) min.pollFirst();
}
// 判断双指针的距离是否为最远
ans = Math.max(ans, r - l + 1);
}
return ans;
}
- 时间复杂度:每个元素最多入队和出队常数次,一共遍历了一次整个字符串,复杂度为 O ( n )
- 空间复杂度:O ( n )
十五、罗马数字转数字
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484403&idx=2&sn=1a8d737b73d779a08b4020f361791a2b&chksm=fd9ca8eccaeb21fa052e9e592150cef10893eb0dc7829667eadf6eddd53ea4f89e4fb80e5a6c&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
- 输入: "III"
- 输出: 3
示例 2:
- 输入: "IV"
- 输出: 4
(1)略解1
主要思路是:判断前面一个或者两个字符,然后将对应的值加到最终结果,再删除那个字符
- 判断前面字符,我想到用的是
string.startWith()方法,但罗马字符的长度不是唯一的,所以删除的时候需要获取当前罗马字符的长度 - 另一种解法就是根据罗马字符的规律。使用 map 获取当前字符和下一个字符的值,然后比较,如果当前字符的值大于下一个字符的值,就取两个字符,否则就取一个字符。
class Solution {
// 设计一个对应关系
Map<String, Integer> map = new HashMap<>(){{
put("M", 1000);
put("CM", 900);
put("D", 500);
put("CD", 400);
put("C", 100);
put("XC", 90);
put("L", 50);
put("XL", 40);
put("X", 10);
put("IX", 9);
put("V", 5);
put("IV", 4);
put("I", 1);
}};
public int romanToInt(String s) {
// n为数组长度
int n = s.length();
int ans = 0;
for (int i = 0; i < n;) {
// 临时字符串
String str = null;
// 比较当前罗马字符的值和下一个罗马字符的值
if (i + 1 < n && map.get(s.substring(i + 1, i + 2)) > map.get(s.substring(i, i + 1))) {
// 取两个字符
str = s.substring(i, i + 2);
i += 2;
} else {
// 取一个字符
str = s.substring(i, i + 1);
i++;
}
// 使用罗马字符对应相关的值
ans += map.get(str);
}
return ans;
}
}
- 时间复杂度:对字符串
s扫描一次。复杂度为 O ( n ) - 空间复杂度:使用了字典记录罗马字符和数值的映射关系,但消耗的空间固定,不随着样本大小而变化。复杂度为 O( 1 )
- 其实难点在于两点:
- 找出当前字符是哪一个罗马字符——使用
string.startWith()或者map.get() - 如何维持循环——取前面的字符,再不断地删除已经取到的字符
- 找出当前字符是哪一个罗马字符——使用
十六、 三数之和
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484423&idx=1&sn=ff37a4bb96de487601d8ea7df59ef794&chksm=fd9caf18caeb260e101a6efe1809663dda5ef7d83d0f8a5df3d7e5e4edb6634f67ea39fab4cf&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0
请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
- 输入:nums = [ -1, 0, 1, 2, -1, -4 ]
- 输出:[ [-1,-1,2], [-1,0,1] ]
示例 2:
- 输入:nums = []
- 输出:[]
提示:
- 0 <= nums.length <= 3000
- -105 <= nums[i] <= 105
(1)略解1
如果直接暴力解法,很简单,但是 30003 = 27000000000 = 2.7 * 1010 ,远大于 107 —— 计算机的 1s 运行时间。
所以需要使用双指针来简化:i 遍历前 n - 2 个字符,然后 j 和 k 在 i 后面进行双指针移动,大于 0 移动 k,小于 0 移动 j。
有没有可能会漏掉一些答案?
假设现在 nums[i] = 0,则需要 nums[j] + nums[k] = 0,假设 k = 19,nums[k] = 9,j = 5,nums[j] = -9。然后当 j 向右移动时,相应的 k 也要向左移动,例如 k = 15,nums[k] = 6,j = 8,nums[j] = -6。
由此可得,j 和 k 会在数组中某一点对称,所以双指针可以找到所有答案。
算法步骤:
- 首先进行 顺向排序(从小到大),因为排序的时间复杂度是 O ( nlogn ) ,而双指针复杂度是 O ( n2), 不用担心排序会影响时间
- 然后固定字符 i ,然后最后一个字符 k 在数组最后面开始向左遍历,计算下一次结果,如果下一次结果大于 0 ,则代表需要继续缩小 k 的值。
- 如果下一次结果(k-1)不大于 0 了,则代表下一次结果可能是目标,则判断
nums[k-1] + nums[j] + nums[i]结果是否等于 0。 - 然后等于 0 的话记录到答案里,并向右移动 j;小于 0 的话,直接向右移动 j 。
- 然后 k 继续向左移动,直到遇到 j 为止。
去掉重复:取到重复情况有两种可能:
- 第 1 个数取到了曾经取到的数
- 第 2 个数取到了曾经取到的数
- 所以如果当前字符和前一个字符相等,则判断下一个字符
总代码如下面所示:
- 第 6 行优化部分:i < n 变成了 i < n-2,少进了两个循环;加上了 nums[i] <= 0 ,因为数组从小到大排序,所以当 i 所指向的数字大于 0 ,就说明 j、k 所指向的数字都大于 0,则三个数加起来不可能等于 0。
public List<List<Integer>> threeSum(int[] nums) {
// 数组排序
Arrays.sort(nums);
int n = nums.length;
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < n - 2 && nums[i] <= 0; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue;
for (int j = i + 1, k = n - 1; j < k; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
while (k - 1 > j && nums[i] + nums[j] + nums[k - 1] >= 0) k--;
if (nums[i] + nums[j] + nums[k] == 0) {
ans.add(Arrays.asList(nums[i], nums[j], nums[k]));
}
}
}
return ans;
}
十七、电话号码的字母组合
原题链接:https://mp.weixin.qq.com/s?__biz=MzU4NDE3MTEyMA==&mid=2247484458&idx=1&sn=f09539514474189d545990987e81c0e4&chksm=fd9caf35caeb2623cff000e51a58b7a5a9b9166064760d2c41dd193ed48fb3b02e574ad350e4&cur_album_id=1715134171561410565&scene=189#wechat_redirect
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例:
- 输入:"23"
- 输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
(1)略解1
这道题第一眼就是使用循环来做,但是循环的次数会根据输入的数字个数改变,所以不能使用循环。
只能使用回溯法(深度优先递归)。回溯法:当前位的字符循环完成后,就回溯到上一个字符继续循环:
这是一道「回溯算法」的经典题。
没有思维的上的难度,考察的是对「回溯算法」的基本理解。
通常我们会如何联想到「回溯算法」呢?基本上对于那些要枚举所有方案的题目,其实都应该先想到「回溯算法」。
「回溯算法」从算法定义上来说,不一定要用 DFS 实现,但通常结合 DFS 来做,难度是最低的。
回溯算法的基本模板是:
- 确定结束回溯过程的基础条件
- 然后遍历所有的 “ 选择 ”
- 对选择进行改变 (做选择 -> 递归 -> 撤销选择)
void dfs(路径, 选择列表, 结果集):
if (满足结束条件) {
结果集.add(路径);
return;
}
for (选择 in 选择列表) {
做选择,修改路径;
dfs(路径’, 选择列表, 结果集);
撤销选择,撤回修改;
}
上面代码中,需要明确几个变量:
路径:路径是得到最终结果前的过程,我们是需要最后拼接成的字符串,所以路径是字符串
选择列表:选择列表用来循环,例如当前数字是 2,则需要循环 【a,b,c】三次,进入三次递归。
如果想知道当前的选择列表,需要知道当前的数字。当前的数字的来源有两个——参数和取原来的字符串。如果来源是参数,则每次都要考虑下一个字符,递归的代码不太雅观。如果是取原来的字符,每次只需要传原来的字符 和 当前递归的层数。
做选择和撤销选择:做选择就是加上字符;撤销选择就是将字符串复原,删除已加上的字符。因为传进来的路径,无论是 String 还是 StringBuilder,内存空间都只有一个,如果不复原,则上层的递归使用的路径是不正确的。
满足结束条件:第 2 点里提到了当前递归的层数,而结束条件就是 i == n(0 ~ n),比原来字符串的长度多一。
结果集:使用的是 ArrayList,这样就不用计算最终数组的长度。
下面为总体代码:
class Solution {
// 定义对应关系
Map<String, String[]> map = new HashMap<>(){{
put("2", new String[]{"a", "b", "c"});
put("3", new String[]{"d", "e", "f"});
put("4", new String[]{"g", "h", "i"});
put("5", new String[]{"j", "k", "l"});
put("6", new String[]{"m", "n", "o"});
put("7", new String[]{"p", "q", "r", "s"});
put("8", new String[]{"t", "u", "v"});
put("9", new String[]{"w", "x", "y", "z"});
}};
public List<String> letterCombinations(String ds) {
int n = ds.length();
List<String> ans = new ArrayList<>();
if (n == 0) return ans;
StringBuilder sb = new StringBuilder();
dfs(ds, 0, n, sb, ans);
return ans;
}
void dfs(String ds, int i, int n, StringBuilder sb, List<String> ans) {
// if (满足结束条件) {
// 结果集.add(路径);
// return;
// }
if (i == n) {
ans.add(sb.toString());
return;
}
// for (选择 in 选择列表) {
// 做选择,修改路径;
// dfs(路径’, 选择列表, 结果集);
// 撤销选择,撤回修改;
// }
// 获取到当前字符
String key = ds.substring(i, i + 1);
// 根据字符获取到选择列表
String[] all = map.get(key);
// 遍历选择列表
for (String item : all) {
// 做出选择
sb.append(item);
dfs(ds, i + 1, n, sb, ans);
// 撤销选择
sb.deleteCharAt(sb.length() - 1);
}
}
}
- 时间复杂度:
n代表字符串ds的长度,一个数字最多对应 4 个字符(7 对应 “ pqrs "),即每个数字最多有 4 个字母需要被决策。复杂度为 O ( 4n ) - 空间复杂度:有多少种方案,就需要多少空间来存放答案。复杂度为 O ( 4n )
该文档完成日期:2022年7月11日